剑指offer面试题

| 分类 interview  | 标签 interview  algorithm 

第25题 二叉树中和为某一值的路径

题目:输入一棵二叉树和一个整数，打印出二叉树中结点值的和为 输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过 的结点形成一条路径。二叉树结点定义如下：

struct BinaryTreeNode
{
    int               m_nValue;
    BinaryTreeNode *  m_pLeft;
    BinaryTreeNode *  m_pRigth;
}

题目中的解法还可以进一步优化，即在查找路径上的和是否与输入的整数相等时，如果还没有到叶结点，而此时路径上的和已经超过输入的整数，就可以直接返回上一结点，不用再判断后续的子结点了。

void FindPath
(
    BinaryTreeNode*   pRoot,
    int               expectedSum,
    std::vector<int>& path,
    int&              currentSum
)
{
    currentSum += pRoot->m_nValue;
    /*
    在此判断currentSum是否大于输入的值，如果大于，就直接跳回父结点
    if(currentSum > expectedSum)
        return;
    
    */
    path.push_back(pRoot->m_nValue);

    // 如果是叶结点，　并且路径上结点的和等于输入的值
    // 打印出这条路径
    bool isLeaf = pRoot->m_pLeft == NULL && pRoot->m_pRight == NULL;
    if(currentSum == expectedSum && isLeaf)
    {
        printf("A path is found: ");
        std::vector<int>::iterator iter = path.begin();
        for(; iter != path.end(); ++ iter)
            printf("%d\t", *iter);
        
        printf("\n");
    }

    // 如果不是叶结点，则遍历它的子结点
    if(pRoot->m_pLeft != NULL)
        FindPath(pRoot->m_pLeft, expectedSum, path, currentSum);
    if(pRoot->m_pRight != NULL)
        FindPath(pRoot->m_pRight, expectedSum, path, currentSum);

    // 在返回到父结点之前，在路径上删除当前结点，
    // 并在currentSum中减去当前结点的值
    currentSum -= pRoot->m_nValue;
    path.pop_back();
}

第26题 复杂链表的复制

题目:请实现函数ComplexListNode* Clone(ComplextListNode* pHead),复制一个复杂链表。 在复杂链表中，每个结点除了有一个m_pNext指针指向下一个结点外，还有一个m_pSibling指向链表中 的任意结点或是NULL。

结点定义如下：

struct ComplexListNode
{
    int                 m_nValue;
    ComplexListNode*    m_pNext;
    ComplexListNode*    m_pSibling;
};

下图为一个复杂链表 复杂链表

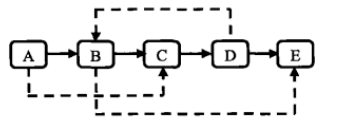
解法

  1. 一般解法：
    1. 复制原始链表上的每个结点，用m_pNext链接起来；
    2. 设置每个结点的m_pSibling指针。假设原始链表中的某个结点Ｎ的m_pSibling指向结点Ｓ，由于Ｓ的位置可能在Ｎ的前面也可能在Ｎ的后面，因此要从原始链表的头结点开始找。沿着m_pNext经过s步找到Ｓ，所以在复制的链表中对应的Ｎ‘也要从头结点沿着m_pNext经过s步。这样就可以设置m_pSibling指针。
    3. 分析，在设置m_pSibling时都要从头结点开始查找，时间复杂度为Ｏ(n^2)
  2. 用空间换时间解法：
    1. 还是按照方法１中的第一步复制链表，用m_pNext链接起来，复制的同时将<N, N’>的配对信息放到一个哈希表中；
    2. 设置结点的m_pSibling。如果原始链表结点Ｎ的m_pSibling指向结点Ｓ，那么在复制链表中，对应的Ｎ‘应该指向Ｓ’。
    3. 通过哈希表可以在Ｏ(1)时间内找到m_pSibling，因此时间复杂度为Ｏ(n)。
  3. 不用辅助空间的解法：
    1. 按照原始链表的每个结点Ｎ复制结点Ｎ‘，把Ｎ’链接到Ｎ的后面。如图所示复制链接
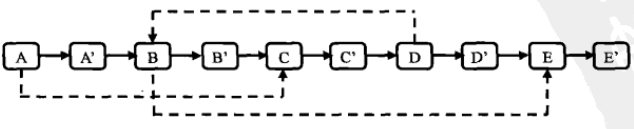
    2. 设置复制的结点的m_pSibling指针。从上图可以看出复制结点Ｎ‘的m_pSibling就是Ｎ的m_pSibling的m_pNext。
    3. 分拆成两个链表，偶数的是新复制的结点，奇数的是原始的链表。
    4. 时间复杂度是Ｏ(n),而且不需要辅助空间。

第29题

Ｏ(n)算法得到数组中任意第K大的数字。

第40题

题目：写一个函数，求两个整数之和，要求在函数体内不得使用+,-,＊，／四则运算符号。

利用位操作：

int add(int num1, int num2)
{
    int sum, carry;
    do
    {
        sum = num1 ^ num2;
        carry = (num1 & num2) << 1;
        
        num1 = sum;
        num2 = carry;
    }while(num2 != 0);
    
    return num1;
}

不使用新变量，交换两个变量的值：

基于加减法 基于异或运算
a = a + b a = a ^ b
b = a - b b = a ^ b
a = a - b a = a ^ b

第50题

树中两个结点的最低公共祖先


上一篇     下一篇